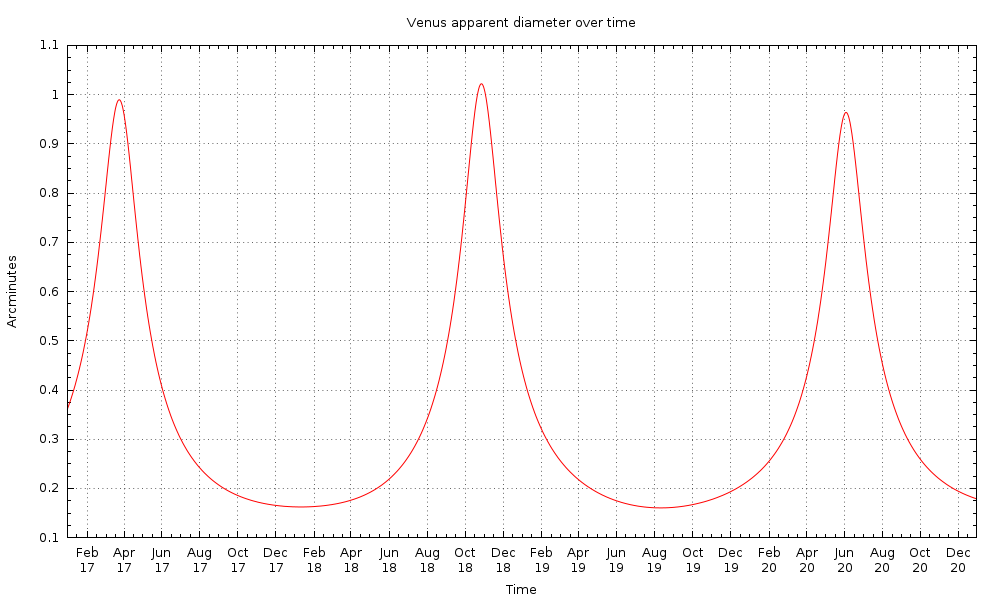
Venus apparent diameter plot for 2017-2020

This blog post was published 7 years ago and may or may not have aged well. While reading please keep in mind that it may no longer be accurate or even relevant.

The apparent size of Venus varies dramatically with the Earth-Venus distance, depending on both orbits around the sun. The apparent angular diameter of Venus is between 0.175 and 1 arcminutes.

Wikipedia has nice images on that and says that…

“the extreme crescent phase of Venus can be seen without a telescope by those with exceptionally acute eyesight, at the limit of human perception.”

I will definitely try next time with my naked eyes, but if you have an entry-level telescope, you will be certainly be better able to see the crescent phase during closest approach.

The question is, when does Venus come closest to Earth for best observation? Not finding anything on the interwebs, I wrote a quick plotting program with Python’s ephem package and gnuplot.

Graph of apparent diameter of Venus in arcminutes for the time period 2017-2020

Here is the very short Python program that calculates the apparent diameter of Venus for 4 years beginning with January 2017:

#!/usr/bin/python3

import datetime as dt
import ephem
import math
from math import radians as rad, degrees as deg

venus = ephem.Venus()

venus_diameter_meters = 2 * 6051800
au_meters = 149597870700

t = dt.datetime.strptime("20170101", "%Y%m%d")

diff = dt.timedelta(days = 1)

for i in range(0, int(4 * 365)):
    venus.compute(t)
    
    dist_venus_meters = venus.earth_distance * au_meters
    
    angular_diameter_arcminutes = 60 * deg(2 * math.asin(venus_diameter_meters / (2 * dist_venus_meters)))
    
    print(t.strftime("%Y-%m-%d"), angular_diameter_arcminutes)
    t += diff

Keywords: pythonastronomy